What Can Polynomial Identities Apply to Beyond Just Polynomials?
Good chore, mathronaut! We're nearly to the pinnacle of Polynomial Mount. At the tiptop we'll plant our Shmoop flag high, snap a few photos to make the folks dorsum home jealous, and discover Pascal's Triangle and the Binomial Theorem.
These are both ways to rapidly multiply out a binomial that'southward being raised past an exponent. Similar, say:
(a + b)0 = 1
(a + b)i = a + b
(a + b)ii = a ii + 2ab + b ii
(a + b)3 = (a + b)(a + b)2 = (a + b)(a 2 + 2ab + b two) = a 3 + iiia 2 b + 3ab two + b 3
And so on. We could go along going all day, just somewhen the exponents would get then big that it would take u.s.a. all day to simplify them. We need a better manner, and luckily a 17th-century French mathematician has already found one.
Blaise Pascal was an interesting dude. He studied physics, philosophy, faith, and mathematics—with maybe just a little aid from alien polynomials from a certain planet. He plant a numerical pattern, chosen Pascal's Triangle, for quickly expanding a binomial like the ones above.

Check it out. The first row is one 1. Then we have ii 1s. After that, things get interesting. The outsides of the triangle are always ane, just the insides are unlike. To find the number on the adjacent row, add the two numbers above it together. See, 2 = 1 + 1; for the row nether that, we accept ane (outer edge), 3 (2 + ane from higher up), 3 (ditto), and 1 (the other border). Every row is built from the row above it.
Pascal's Triangle gives u.s.a. the coefficients for an expanded binomial of the form (a + b) due north , where n is the row of the triangle. The Binomial Theorem tells the states we can utilize these coefficients to discover the entire expanded binomial, with a couple extra tricks thrown in.
What almost the variables and their exponents, though? Continue your pants on; the Binomial Theorem has us covered. At the left side of the triangle, nosotros have anorthb 0 = an . As we motion to the right, we subtract 1 from a's exponent and add it to b'south. It's like b keeps stealing exponents from a, 1 at a time, until he'southward got them all. That sneaky devil.
Pascal doesn't tell us about the sign of each term, though. Luckily, our polynomial friends have us covered. We're getting covered a lot here, aren't nosotros?
Anyhow, when a binomial has a "+" sign, such as (a + b)2 , all of the terms of the expansion are positive.
When we expand a binomial with a "–" sign, such equally (a – b)5 , the kickoff term of the expansion is positive and the successive terms will alternate signs.
With all this help from Pascal and his good buddy the Binomial Theorem, we're ready to tackle a few problems.
Sample Problem
Aggrandize (x – y)4.
Have a await at Pascal's triangle. From the fourth row, we know our coefficients volition exist i, iv, 6, four, and 1. That negative sign ways that the outset term of our expansion will be positive, and the following terms will alternate signs. The exponents will start at 10 4 y 0 and move to ten 3 y 1, etc.
(x – y)4
= 1x 4 – 4x three y + 6ten 2 y two – 4xy 3 + aney 4
= x 4 – ivx 3 y + 610 2 y ii – 4xy 3 + y iv
Wasn't that much easier than trying to multiply the expression out? Nosotros probably wouldn't accept even tried, no affair how much the polynomials complained to us.
Sample Problem
Aggrandize (m + 2n)five.
Have Pascal, will travel (all the way to the answer). Our coefficients are one, 5, 10, ten, 5, 1. The 2northward doesn't change anything; treat information technology like a single term.
1m 5 + vm 4(2n) + xm iii(iin)2 + 10chiliad two(2north)3 + vthousand(2n)4 + 1(iinorthward)5
= thou 5 + tenm four n + 40one thousand iii n 2 + 80k 2 n 3 + lxxxmn 4 + 32north 5
With Pascal on our side, nosotros feel invincible. Even so, that isn't quite the instance. We're withal weak to bullets, being dipped in lava while a villain monologues at us, or a well-timed chocolate. Nosotros besides have trouble dealing with very large exponents; for every row nosotros add together to Pascal'due south triangle, information technology takes longer and longer to find the next. We besides tin't afford to skip whatever rows, or the usher volition escort us out.
Oft times, when we have a binomial with a huge exponent, we only need one or a few terms. For those problems, we'll use a special formula. Information technology allows us to discover the coefficient of but 1 specific term without finding any of the others.
It looks pretty weird, simply stay with usa.

Whew, that affair looks beastly. But dreadful. It has fractions and exponents and factorials. We haven't fifty-fifty mentioned even so that the formula doesn't fifty-fifty tell you lot the sign of the term, either.
To find the r th term of a binomial expansion (a + b) northward , plug the terms into the formula.
If the binomial has a "+" sign, then all terms found using this formula are positive.
If the binomial has a "–" sign, then the term is negative if r is even. If r is odd, then the term is positive.
Maybe information technology won't be then bad once we solve a trouble or two with it. Don't judge a volume-sized formula by its cover, eh?
Sample Problem
Find the 12th term of (x – y)14.
That binomial would take forever to multiply out, and we'd make hundreds of mistakes while doing it anyway. We're convinced already; requite the states the new formula, please.
Allow's run into: r = 12 and n = 14, while a = ten and b = y. The 12th term is even, so our term will be negative.

Call back, a factorial is a shortcut for writing a agglomeration of multiplication, like 3! = three × ii × 1. That means we can cancel out a lot of that 14! with the 11! below it, since 14! = 14 × 13 × 12 × eleven!

Okay, nosotros were skeptical at first, simply this wasn't actually too bad. As long as we know the formula, it works out.
Sample Problem
Discover the 7th term of (x + y)17.
This is it—the last trouble before the pinnacle of Polynomial Mountain. We've come up a long way, so let'south push just a petty further.
Nosotros accept an r of 7 and an due north of 17. The term volition be positive because nosotros've got a plus sign in our binomial, so all the terms are gonna be positive.
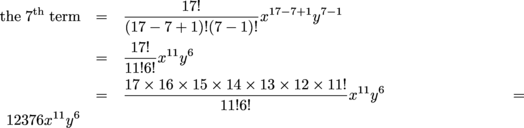
Just think of how many terms we'd have to add together together to become a number like 12,376 out of Pascal's Triangle.
With that out of the way, we've fabricated it to the meridian. We've conquered Polynomial Mountain by learning the polynomials' ways, living amongst them, and befriending them in their alien habitation. Until next time, mathronauts!
Source: https://www.shmoop.com/study-guides/math/polynomial-equations/polynomial-identities
0 Response to "What Can Polynomial Identities Apply to Beyond Just Polynomials?"
ارسال یک نظر